エラトステネスの篩を実装してみた[python]

皆さんこんにちは！タカモリです。 前回、素因数分解のアルゴリズムを記事で書いた際に、素数判定のアルゴリズムのうちできるだけ簡単そうなアルゴリズムを掲載してみたのですが、コメントで「エラトステネスの篩を調べてみると良いよ！」と声をいただきましたので、今日は少し寄り道をしてエラトステネスの篩を実装してみた記事を書こうと思います。

エラトステネスの篩とは

僕も知らなかったのですが、エラトステネスの篩とはN以下の素数を判定するためのアルゴリズムの一つみたいですね。

やり方としては、例えば1000以下の素数を調べたい場合に、2から順番にその数が素数かどうかを調べ素数であれば素数として保存します。この場合は2は素数なので素数として保存します。

そして1000以下のその素数の倍数を順に素数リストから弾きます。2の場合は4・6・8・10の順に1000までの2の倍数を倍数を素数ではないと判断します。(具体的なやり方は後述します。)

2の次は3ですが、3も2と同様に素数ですので素数として保存し、その倍数6・9・12を素数リストから弾きます。

続いて4ですが、これは既に2の倍数ですので素数リストから弾かれているので次の5に進みます。

といった具合に、2からNまでを小さい数時の倍数を素数から弾き残ったものを素数として判定する方法です。

エラトステネスの篩のアルゴリズム

1. まずはN分の要素を持つ配列を用意します。1000までの素数を判定したい場合は1000要素が入る配列です。

2. その配列の0番目(数字としては1になるので少しややこしい。。)の要素にfalseを以降に全てtrueを入れます。こうすることで1に対応した配列の要素はfalseに、2から1000までに対応した配列の要素はfalseになります。[false, true, true, true, true...]

3. 配列を回し、配列の要素がtrueになった箇所に対応する数を素数として保存し、その数の倍数に対応する配列の要素をfalseに変えます。

pythonで実装してみた

これについても実装方法は人それぞれな感じだったので、それっぽいロジックを作ってみました。変だよ・・・とかあったら教えてくださいね！

def eratosutenesunohurui(self, num):
        array = []
         # 配列の一番目をFalseに
        array.append(False)
        for i in range(1, num):
            array.append(True)

        sosuu = []
        for confirme_number, confirme_boolean in enumerate(array):
            if confirme_boolean == True:
                prime = confirme_number + 1
                sosuu.append(prime)
                for j in range(prime, num + 1, prime):
                    if j != prime:
                        not_prime = j - 1
                        array[not_prime] = False
        
        return sosuu

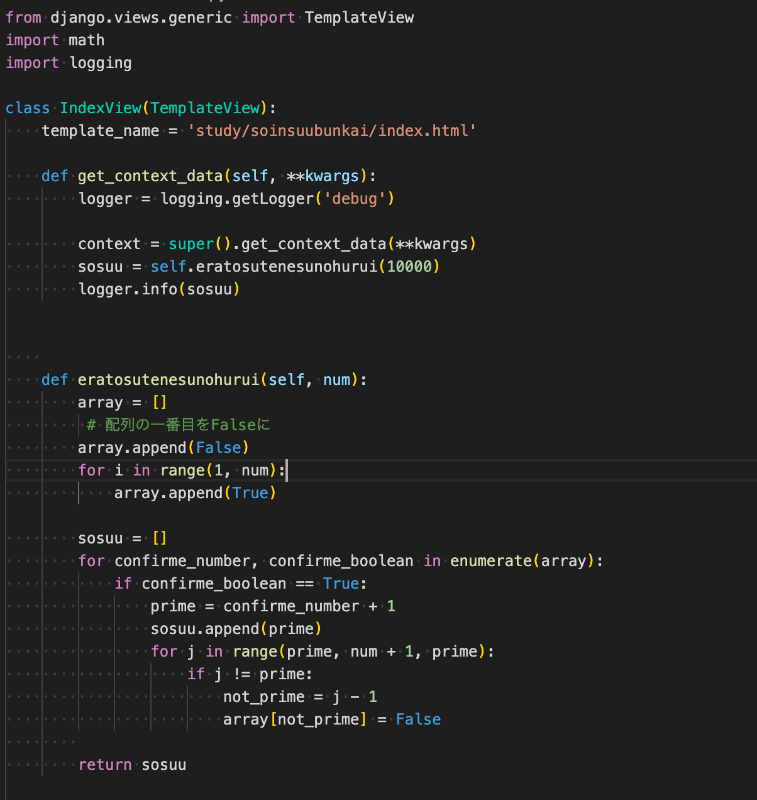
少し分かりにくいかもですが、1000までの素数を選別しています。数字は端っこ切れてますが・・・ というわけで今回はエラトステネスの篩を実装してみました！ これは果たして中学校数学なのか？・・

ではまた！