こんにちは！タカモリです。 今日は「論理演算」と合わせて「ベン図」について一緒に勉強していきましょう！

まず論理演算について見ていきます。

論理演算

論理演算とはその条件を真(true)または偽(false)の2つの値で行う演算のことです。プログラミングをやったことある方であればここは馴染み深いですね！

まずここに、複数のカタカタくんを用意しました。

これらのカタカタくん達はそれぞれ以下に分類されます。

1. 鍋好きなカタカタくん
2. プログラミングが好きなカタカタくん
3. 鍋とプログラミングどちらも好きなカタカタくん
4. 鍋もプログラミングも好きではないカタカタくん

ではこのカタカタくん達を使って「鍋好きなカタカタくん」という条件に対しtrueかfalseでその条件が成立しているかを演算します。 しかし、今の例のように条件が一つであればいいのですが、条件が複数ある場合などに用いられる「AND」や「OR」・「NOT」などの論理演算がありますのでそれを見ていきたいと思います。

論理積(AND)

論理積はOOかつOOである。というように、その両方の条件が一致するものとなります。例えば「鍋好き」かつ「プログラミング好き」みたいな感じですね。この条件がどちらも満たされていれば演算結果は真(true)となります。

論理和(OR)

論理和はOOまたはOOである。というように、その両方のうち片方の条件が一致する(両方一致する場合を含む)ものとなります。例えば「鍋好き」または「プログラミング好き」の場合、プログラミングが好きでなくても鍋が好きであれば演算結果は真(true)になります。またプログラミング好きであっても鍋が嫌いな場合や、鍋とプログラミングどちらも好きである場合も演算結果は真(true)となります。それ以外の場合は偽(false)となります。

否定(NOT)

否定は上の2つと違い入力が一つの単行演算です。これはその条件に合致しない場合に真(true)となります。なので「鍋好き」の条件式の時は、鍋が好きでない時のみ真(true)となります。 これは比較的分かりやすいのではないでしょうか。

ベン図

上で説明した論理演算を図に表したものがベン図です。学校でも習うらしいのですが少なくとも僕は「記憶にございません。」

先ほどの論理演算をベン図に表したものを見ていきましょう！

論理積(AND)

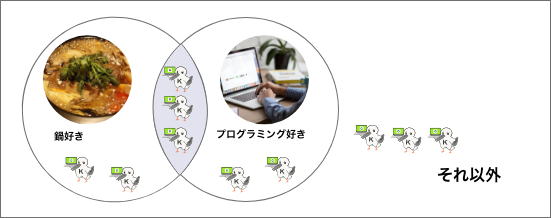
論理積はOOかつOOが成立しているなら真でした。つまりベン図ではこうなります。2つの円が重なった色のついた部分が真それ以外が偽となります。 鍋とプログラミング両方好きなカタカタくんが真となります。

論理和(OR)

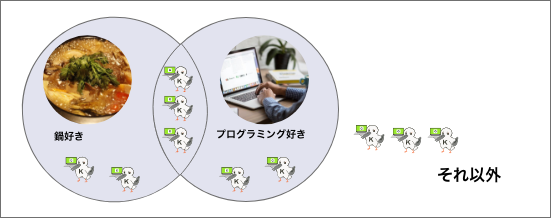
論理和はOOまたはOOが成立している場合でしたね！どちらも成立している場合も真となりますのでベン図ではこうなります。 鍋好き・プログラミング好き、またはそのどちらも好きなカタカタくんが真となります。

否定(NOT)

最後に否定です。これは鍋好きなカタカタくん以外が真となりますのでベン図ではこうなります。分かりやすいですね！

ということで今回は論理演算とベン図について見ていきましたが、大体イメージは着きましたでしょうか？次回はこの知識を使って更に先に進んでいきましょう！