加算器
こんにちわ!タカモリです。今回は加算器について学習していきたいと思います。
コンピュータは 0 + 1 や 1 + 1 などの2進数を足し算によって計算する機械だということは、以前学習しましたね! 前回、演算する為の回路について学習しました。その演算する為の回路を更に組み合わせ、足し算をする為の回路としたのが「加算器」です。
ではまず、2進数の足し算のパターンについて見ていくと
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10
これらの4パターンが2進数の足し算としてあるかと思います。そしてこの4パターンのうち、4番目のみが次の桁に繰り上がることになるのはお分かりだと思います。
では、101 + 101 のように3桁の足し算について考えてみます。分かりやすいように筆算で見てみると
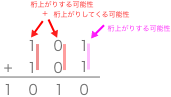 1桁目ピンクの列については、次の桁に繰り上がる可能性があります。そして2桁目と3桁目の列は、桁上がりする可能性と桁が上がってくる可能性を考慮しなければなりません。
1桁目ピンクの列については、次の桁に繰り上がる可能性があります。そして2桁目と3桁目の列は、桁上がりする可能性と桁が上がってくる可能性を考慮しなければなりません。
この、一つ下の桁から繰り上がる可能性がない1桁目に使用される加算器を「半加算器」その可能性を考慮したものを「全加算器」と言います。
半加算器
ではまず半加算器の仕組みから見ていきましょう。今まで学習した論理回路をどのようにすれば加算器を作れるかを考えていきます。
分かりやすいように筆算にすると。
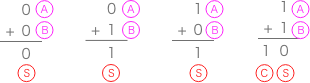
繰り上がる可能性があるので、入力Aと入力Bの時に出力Sと出力Cそれぞれ別々の真理値表で確認して見ましょう。
まずは入力Aと入力Bの時の出力Sの時の真理値表です。
| 入力A | 入力B | 出力S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
そのまま当てはめて見ましたがどうでしょうか?Cを考えずにSだけ見ればこのようになるかと思われます。続いて入力Aと入力Bの時の出力Cを真理地表で見てみましょう。
| 入力A | 入力B | 出力C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
繰り上がる時のみ1が発生するので、それ以外は0ですね!これも大丈夫そうですね!
実はこの出力Sに対する真理値表は論理回路で学習した「排他的論理和回路」、出力Cに対する真理値表は論理積回路と同じなのですね!
これを組み合わせることで半加算器が出来上がります。
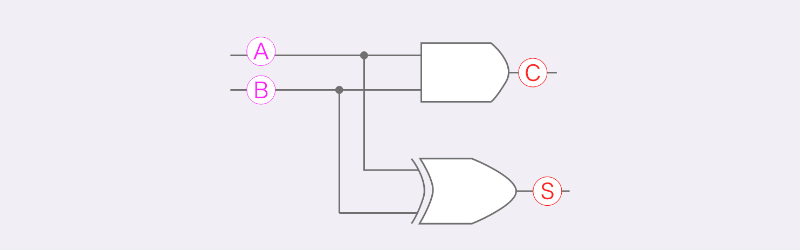
全加算器
続いて全加算器についてみていきます。半加算器は一つ下の桁からの繰り上がりに対応できていなかったので、全加算器はそれに対応する必要があります。
なので、半加算器で出力した結果と繰り上がってきた数を最度半加算器で足してあげる必要があります。 半加算器を2つ繋げたので出力側のCが二つできることとなりますが、これは論理和回路で繋げてあげます。
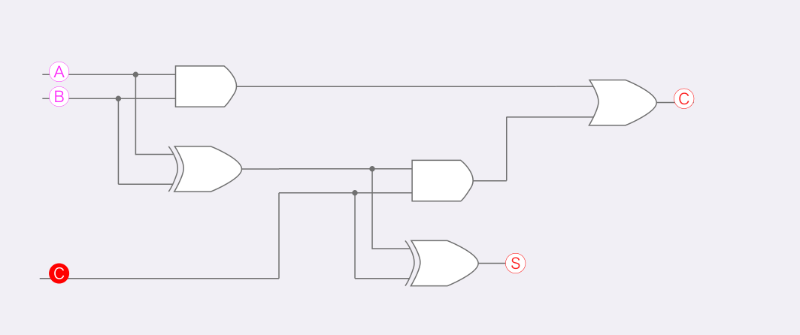
これで下の桁からの繰り上がりに対応した全加算器の完成です。結構ゴツくなりましたね笑 図でもAB以外に赤く塗りつぶしたCからの値を受け取ることができることに気がつくと思います。
なるほどですね。このようにコンピュータは足し算をする仕組みになっているのですね!今回は以上です。お疲れ様でした!


