固定小数点数と浮動小数点数
こんにちは!タカモリです。2進数の計算方法について前回までにブログで書き起こしましたが、今回は2進数の小数点に関して書いていきたいと思います。
コンピュータは数を表す方法に、固定小数点数と浮動小数点数があります。それぞれ全く異なった数の表現方法ですので、早速順番に見ていきましょう!
固定小数点数
例えば8ビットで小数点付きの数を表す場合には、どのビットとどのビットの間に小数点を置くのかということが問題になるかと思われます。例えば11111111これは10進数の255という数字ですが、111111.11と6ビット目と7ビット目の間に小数点を置いた場合、10進数では63.75という全く異なった数字になるかと思われます。
このように、予め小数点の箇所をあらかじめルールに定めた箇所(この場合では6ビット目と7ビット目の間)に配置する方法を固定小数点数と言います。
しかし、上で見た通り固定小数点数の場合1000000000000や0.000000000001などの無駄に桁数が多い数を表す為には限られたビット数しかない為、対応することができません。これはなんとなくわかりますよね。
なので上の数のように無駄に多くの桁数を必要としない数に固定小数点数は使われます。例えば小数点がない整数15の場合2進数では00001111ですが、この8ビット目より後ろに小数点があると考え固定小数点の一種と言えます。
固定小数点数で表せる数
固定小数点数で表せる数はそのビットで表せる単純なもので、先頭に符号ビットがある場合とない場合で表すことのできる数にも差が出ます。
| 符号ビットなし | 2進数 | 10進数 |
|---|---|---|
| 最小 | 00000000 | 0 |
| 最大 | 11111111 | 255 |
| 符号ビットあり | 2進数 | 10進数 |
|---|---|---|
| 最小 | 10000000 | -128 |
| 0 | 00000000 | 0 |
| 最大 | 01111111 | 127 |
符号ビットありの最小値は最大値と一致位しないことに注意が必要ですね! 固定小数点数は計算の精度が低いものの、高速に処理できるというメリットがあります。
なおどれくらい差が出るのかについては私にはわかりません笑
浮動小数点数
先程の固定小数点数は桁数の大きな数には不向きなものでした。しかしこの浮動小数点数で数を表せば大きな桁数を持つ数を表すことができるようになるのです。ではその仕組みにいついて見ていきましょう。
例えば10進数の0.0020という小数点のある数字があるとします。この数は小数点を移動させることで000.20 × 10の2乗と同じ数と言えると思います。これを指数表記と言いますが、浮動小数点数を表す為にはこの指数表記を使います。
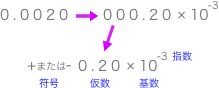 上の図は基数を10で考えたものですが、2進数の場合基数はもちろん2になります。そして小数点の位置が右に2つずれていますね!
上の図は基数を10で考えたものですが、2進数の場合基数はもちろん2になります。そして小数点の位置が右に2つずれていますね!
浮動小数点数では上の図にある符号 仮数 基数 指数それぞれの値をビットに当てはめて数を表します。
では、どのようにビットに当てはめていくのかを見ていきましょう。当てはめ方には種類があるのですが まずは32ビットの例から見ていきます。
普通の32ビットの形式例
ここに32ビットの形式の図があります。上で説明したように32ビットを符号部、指数部、仮数部とわけ、それぞれにビットを割り振ります。
 それではこの形式を使って、10進数の0.375という数字を当てはめた場合を見ていきます。
0.375は2進数の0.011ですこれを指数表記に直すと0.11 × 2の-1乗という形になります。この時の符号は正の数なので「0」仮数は「11」指数は「-1」となります。ただし指数はマイナスの値なのでこの場合補数「11111111」となります。それではこれを32ビット形式に当てはめましょう。
それではこの形式を使って、10進数の0.375という数字を当てはめた場合を見ていきます。
0.375は2進数の0.011ですこれを指数表記に直すと0.11 × 2の-1乗という形になります。この時の符号は正の数なので「0」仮数は「11」指数は「-1」となります。ただし指数はマイナスの値なのでこの場合補数「11111111」となります。それではこれを32ビット形式に当てはめましょう。
 当てはめた後、仮数部の余った部分には0を埋めて完成です。どうでしょうか?これで少しはイメージができたのではないでしょうか?続いて別の形式を見ていきたいと思います。
当てはめた後、仮数部の余った部分には0を埋めて完成です。どうでしょうか?これで少しはイメージができたのではないでしょうか?続いて別の形式を見ていきたいと思います。
IEEE754の形式例
もう一つはIEEEにより規格化されたIEEE754という規格です。こちらは通常の32ビットの形式と比べ同じ32ビットを更に効率よく使えるように工夫されています。
では早速見ていきます。
 通常の32ビットの形式と違うのは、指数部が1ビット分追加され仮数部が1ビット少ない23ビットで構成されているという点です。しかし先程の上で利用した0.375の2進数0.11を1.1とし、更に先頭の1を省略することで24ビットと同じ表現をすることができます。
通常の32ビットの形式と違うのは、指数部が1ビット分追加され仮数部が1ビット少ない23ビットで構成されているという点です。しかし先程の上で利用した0.375の2進数0.11を1.1とし、更に先頭の1を省略することで24ビットと同じ表現をすることができます。
そして指数部についても通常の32ビット形式と違う点があります。通常の指数部では指数がマイナスの場合にその指数の補数を指数部に当てはめて表現していましたが、IEEE754の場合は指数に127をプラスする(バイアス)することで負の数、正の数に関わらず、全て正の数で指数を表現することができるようになっています。
では先程と同じように0.375を実際にIEEE754形式に当てはめていきましょう。 0.375の2進数0.011を先程とは違い1.1 × 2の-2乗に変換します。この時の符号は正の数なので「0」、仮数は「1」、そして指数は-2に127を足した数を2進数に変換します。つまり125の2進数「01111101」です。
それでは、先程と同じようにこれを当てはめていきましょう!
 当てはめること自体は先程と変わらないのですが、やはり途中の計算方法に若干違いがあるというのがポイントでしょうか。
当てはめること自体は先程と変わらないのですが、やはり途中の計算方法に若干違いがあるというのがポイントでしょうか。
こういう仕組みで、パソコンは大きな数字を扱っていたのですね。人間の知恵が詰まっていて感動モノですね!とは言いながらもやはりややこしい。。僕も小数点についてはかなり戸惑いました(戸惑ってばっかり)しかし一つ一つ整理することで意味がわかってくるようになると思うので一緒に頑張っていきましょう!


